The given equation is the quadratic equation. The degree of the equation is two. So, we can solve the equation using a quadratic formula and factorization method. We will use the factorization method to find roots.
What are the roots of x2-11x+28=0?
x2– 4x- 7x+ 28 =0
x(x-4) – 7(x-4) =0
(x-4) (x-7) =0
x=4, x=7
So, the roots of the given quadratic equation are “4” and “7”.
Modulus | |;
The mod of 4 and 7 is |4 − 7| is “3”.
The mod of 7 and 4 |7 − 4| is “‘3”.
The value of mod is always positive.
Verification of roots;
How we will come to know about the correction of roots?
How we will verify our roots?
Is our solution correct?
To clear all the confusion, we will verify the roots. The number “4” is the correct root if it satisfies the given equation. To satisfy, we will put x=4 into the given equation and if the left-hand side is also zero, then we have to find out the correct root.
42-11(4)+28=0
16-44+28=0
28-28=0
0=0
So, 4 is the correct root. Similarly, you can check for the other root.
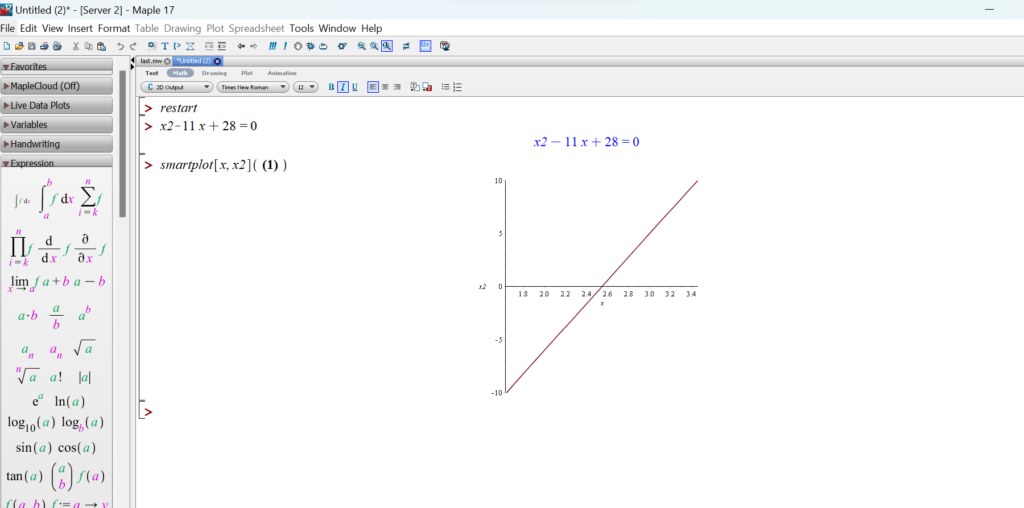
Graph of x2-11x+28=0?
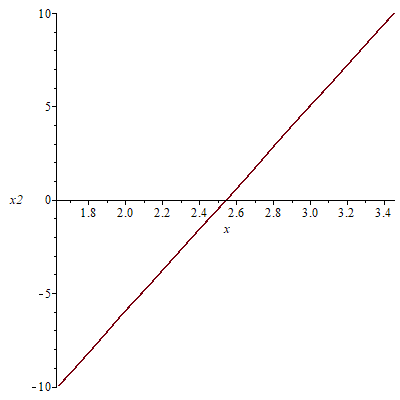
We can find 2D and 3D graphs using different software. I have plotted this graph using Maple.